Another Fun round of Math!
I know math is not the fun class but I am really enjoying study the subject this year, within 2018 – 2019 I got to learn about Precalculus, which includes algebra and trigonometry at a level which is designed to prepare students for the study of calculus. Ever thought, algebra and trigonometry is not my strength I still want to build those skill into my strength. This round we are studying in Chapter 3 (Polynomial and Rational Functions), which include seven smaller subjects. I would like to show some example in the small subjects that related to Chapter 3.
In Chapter 3.2 (Polynomial Functions and Their Graphs) we learn the polynomial functions simply as polynomials. The following polynomial has degree 5 leading coefficient 3, and constant term -6
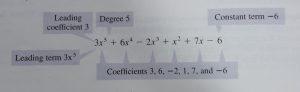
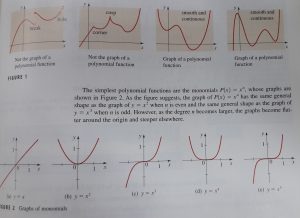
We also need to understand how the graph of a basic polynomial function look like and which graph is not a polynomial function.
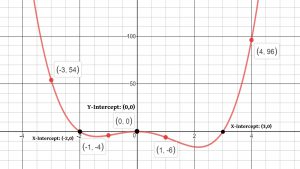
Example: P(x)=x^4 − x^3 − 6x^2
First, we’ll need to factor this polynomial as much as possible so we can identify the zeros and get their multiplicities.
P(x )= x^4 − x^3 − 6x^2 = x^2(x^2 − x − 6) = x^2(x − 3)(x + 2)
Here is a list of the zeroes and their multiplicities.
X = −2 (multiplicity 1)
X = 0 (multiplicity 2)
X = 3 (multiplicity 1)
So, the zeros at x = -2 and x = 3 which will correspond to x-intercepts, that cross the x-axis since their multiplicity is odd. The zero at x = 0 will not cross the x-axis since it multicity is even. The y-intercept is (0,0) and notices that this is also an x-intercept.
The coefficient of the 4th-degree term is positive and so since the degree is even we know that the polynomial will have a positive infinite bound at both ends of the graph.
Finally, here are some function that helps to the graph, We need to plug in a random number to help identify the behavior of the graph. Normally, we would have one point in between the zeros.
P(−3) = 54
P(−1) = −4
P(1) = −6
P(4) = 96
Here is a sketch of a graph